Project Title:
KENET: CS-IS-EE RF Radiation Activity 2G+, Wi-Fi, IoT 2020, HEALTH Studies.
RF Calculators
Skin Depth
Skin depth is dependent on the frequency of the current/signal and the resistivity of the material. It inversely proportional to the
frequency and directly proportional to the resistivity.
Normally denoted as δ and defined in units of meters[m], skin depth
is given by the equation:
[m]
With respect to conductivity as an inverse of resistivity, skin depth can be determined as:
[m]
where:
ƒ: frequency of the source [Hz]
μ: magnetic permeability of material [H/m]
σ: conductivity of the medium [S/m]
ρ: resistivity of the medium [Ω.m]
It is a measure of the current density, and is defined as the distances from the outer edges of a conductor to the point at which the current density falls to 1/e of the value at the surface
Free Space Path Loss [FSPL] Calculator
FSPL is the loss in signal strength as it travels through free space. This value is usually calculated by discounting
any obstacles or reflections that might occur in its path. IEEE defines it as The loss between two isotropic radiators in free space, expressed as a power ratio.
It is expressed in dB.
where
d: Distance between the antennas [m]
f: operating frequency [Hz]
GTX: Gain of transmitting antenna [dB]
GTR: Gain of receiving antenna [dB]
c: Speed of light in vacuum[m/s]
The free space path loss is used to predict the strength of a RF signal at a particular distance. This is a theoretical value, as in the real world, there are many obstacles, reflections and losses which need to be accounted for when estimating the signal at a location. However the FSPL is a good approximation for estimating the loss of signal when propagating through free space.
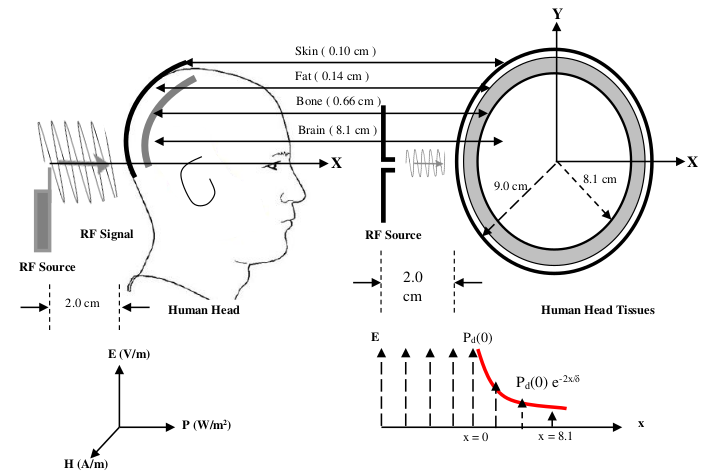
Human Head-RF Source Modeling
In order to assess human exposure to RF electromagnetic fields, it is required to
construct an appropriate model of a human head and the RF source (phone).
Considering a human head modeled as a four-layer structure that consist of
skin, fat, skull and brain.
The human head biological tissues may be considered as lossy dielectric materials with
permeability equal to free space permeability(μ=μo),and conductivity that depends on tissue
properties and signal frequency.
For instance consider a mobile phone assumed to be in transmit
mode, that transmits RF energy in a single direction towards the head as it is assumed to be
located 2 cm away from the human head. The human head model is as shown:
Reference:Godra, L. Chand, Handbook
Body Tissues Dielectric Properties
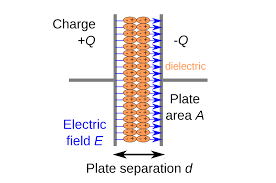
A dielectric (or dielectric material) is an electrical insulator that can be polarized by an applied electric field. When a dielectric material is placed in an electric field, electric
charges do not flow through the material as they do in an electrical conductor but only slightly shift from their average equilibrium positions
causing dielectric polarization.
Because of dielectric polarization, positive charges are displaced in the direction of the field and negative charges shift in the direction opposite to the field (for example, if the field is moving in the positive
x-axis, the negative charges will shift in the negative x-axis). This creates an internal electric field that reduces the overall field within the dielectric itself.
If a dielectric is composed of weakly bonded molecules, those molecules not only become polarized, but also reorient so that their symmetry axes align to the field.
The study of dielectric properties concerns storage and dissipation of electric and magnetic energy in materials.
Dielectrics are important for explaining various phenomena in electronics, optics, solid-state physics, and cell biophysics.
Definitions
- electrical insulator
- electrical insulator > An electrical insulator is a material in which the electron does not flow freely or the atom of the insulator have tightly bound electrons whose internal electric charges do not flow freely; very little electric current will flow through it under the influence of an electric field.
- electric field
- electric field > An electric field (also termed as E-field) is the physical field that surrounds each electric charge and exerts force on all other charges in the field, either attracting or repelling them. It originate from electric charges, or from time-varying magnetic fields.
- electrical conductor
- electrical conductor > A conductor is an object or type of material that allows the flow of charge (electrical current) in one or more directions. Materials made of metal are common electrical conductors. Electrical current is generated by the flow of negatively charged electrons, positively charged holes, and positive or negative ions in some cases.
- polarization
- polarization > Polarization density (or electric polarization, or simply polarization) is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is said to be polarized. The electric dipole moment induced per unit volume of the dielectric material is called the electric polarization of the dielectric
Where:
σ: tissue conductivity [S/m]
md: tissue mass density [Kg/m3]
εr: tissue relative permittivity.
Specific Absorption Rate (SAR)
(Basic calculator)
SAR is a unit of measurement for the amount of radio frequency energy absorbed by the body when using a wireless device.
It is determined as:
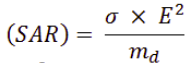[W/Kg]
The tissue power density is defined as:
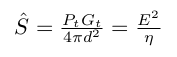[W/m3]
where
md: tissue mass density [Kg/m3]
σ: Conductivity [S/m]
E: electric field intensity [V/m]